题目描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
和爬楼梯是一样的题目
示例 1:
输入:n = 2
输出:2示例 2:
输入:n = 7
输出:21示例 3:
输入:n = 0
输出:1提示:0 <= n <= 100
1 | class Solution { |
方法一:动态规划
此类求 多少种可能性 的题目一般都有 递推性质 ,即 f(n) 和 f(n-1)…f(1) 之间是有联系的。
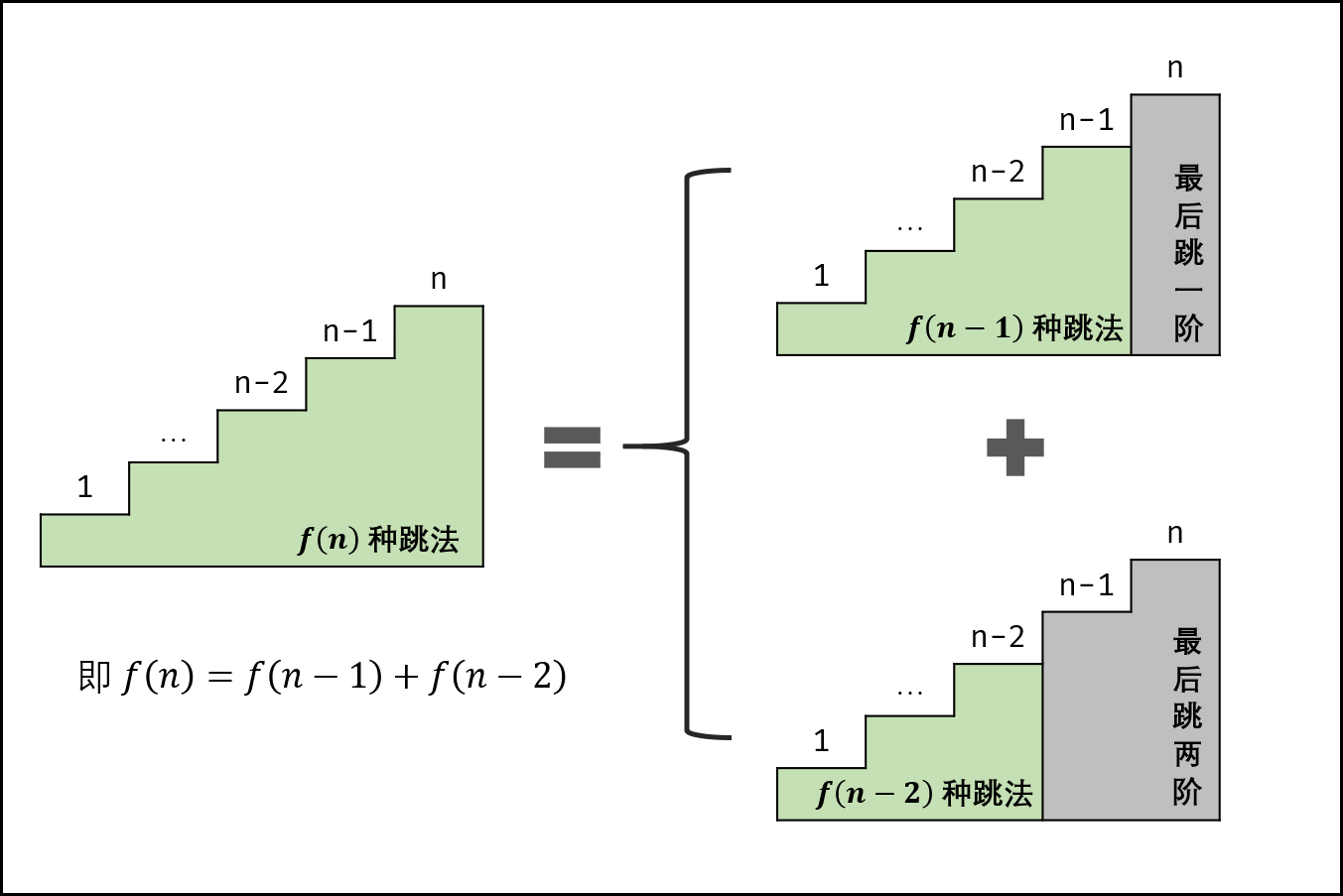
设跳上 n 级台阶有 f(n) 种跳法。在所有跳法中,青蛙的最后一步只有两种情况: 跳上 1 级或 2 级台阶。
当为 1 级台阶: 剩 n-1 个台阶,此情况共有 f(n-1) 种跳法;
当为 2 级台阶: 剩 n-2 个台阶,此情况共有 f(n-2) 种跳法。
f(n) 为以上两种情况之和,即 f(n)=f(n-1)+f(n-2) ,以上递推性质为斐波那契数列。本题可转化为 求斐波那契数列第 n 项的值 ,与 斐波那契数列 等价,唯一的不同在于起始数字不同。
- 青蛙跳台阶问题: f(0)=1,f(1)=1,f(2)=2;
- 斐波那契数列问题: f(0)=0,f(1)=1,f(2)= 1
1 | // 原动态规划 空间复杂度为 O(n) |
复杂度分析:
- 时间复杂度:O(N),计算 f(n) 需循环 n 次,每轮循环内计算操作使用 O(1)
- 空间复杂度:O(1),几个标志变量使用常数大小的额外空间
执行结果:通过
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:36.2 MB, 在所有 Java 提交中击败了81.08%的用户
变形:不能跳到7与7的倍数的台阶
1 | // class Solution { |
变形:不能连续跳两个台阶
题目里“不能连续跳两个台阶”,即一旦跳了两个台阶,则下一步只能跳一步(2->1),把它们连在一起就一共跳了三个台阶,所以问题可以转化为要么跳一个台阶,要么跳三个台阶(当然还是有点区别的,只不过因为结果是一样的,所以可以这么转化),于是就有了 f(x) = f(x-1) + f(x-3)
1 | public int climbStarts2(int n) { |